Markdown macros for Typora
注意括号的 4 个只有 Typora 能用,因其较为特别的 MathJax 配置。
不建议用这 4 个,如果你不只用 Typora 的话。
注意括号的 4 个只有 Typora 能用,因其较为特别的 MathJax 配置。
不建议用这 4 个,如果你不只用 Typora 的话。
Gyula Konig proposed the following paradox: By the Well Ordering Theorem, the real number set \(\mathbb{R}\) can be well ordered. We study the elements of \(\mathbb{R}\) and classify them. If a real number can be defined using a finite number of symbols, then we say it is finitely definable. Otherwise, we say it is undefinable. Obviously, undefinable real numbers exist, because finitely definable real numbers must be countable, while \(\mathbb{R}\) is uncountable. It is also obvious that, in the well order, the "smallest" elements, i.e., the beginning elements, are finitely definable. So the question is where we can find the first undefinable number. If \(x\) is the first undefinable number, then its immediate predecessor is finitely definable. However, the above relationship with a finitely definable number should make \(x\) finitely definable as well.
How do you think of this paradox? Write an essay of no more than 1000 words.
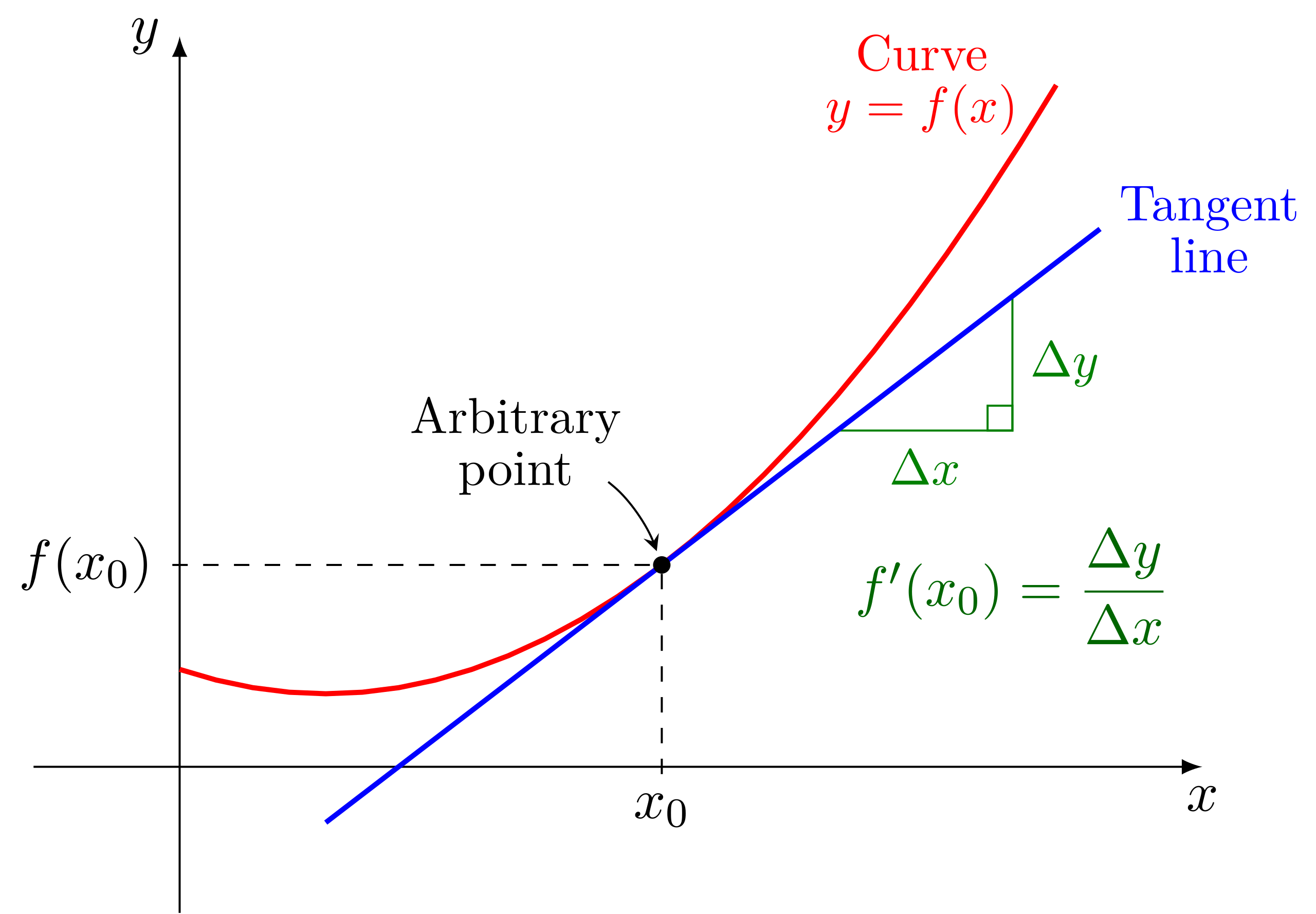
An archive of MIT 18.01SC Single Variable Calculus Fall 2010 with organized notes, problem sets and exams.