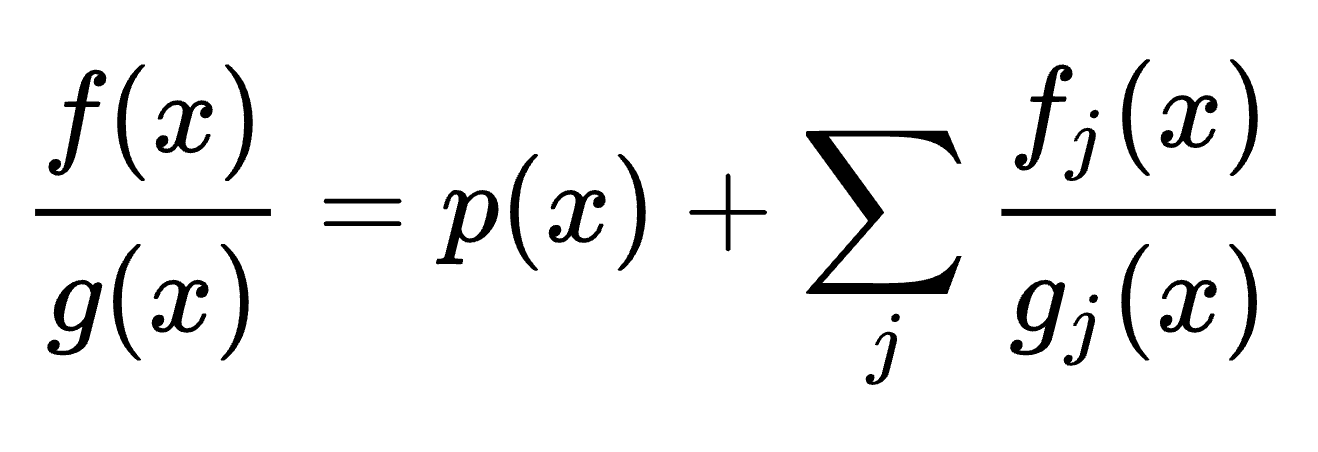Home¶
Welcome to my new blog!
把博客迁移到 Material for Mkdocs 上啦
应该会看起来正经一点（？然后可能会尝试一些自定义的 CSS，也许会比较好看吧。
Cry..
花了几个小时写 CSS..
The Storm in Foundational Mathematics: König's Paradox
Gyula Konig proposed the following paradox: By the Well Ordering Theorem, the real number set \(\mathbb{R}\) can be well ordered. We study the elements of \(\mathbb{R}\) and classify them. If a real number can be defined using a finite number of symbols, then we say it is finitely definable. Otherwise, we say it is undefinable. Obviously, undefinable real numbers exist, because finitely definable real numbers must be countable, while \(\mathbb{R}\) is uncountable. It is also obvious that, in the well order, the "smallest" elements, i.e., the beginning elements, are finitely definable. So the question is where we can find the first undefinable number. If \(x\) is the first undefinable number, then its immediate predecessor is finitely definable. However, the above relationship with a finitely definable number should make \(x\) finitely definable as well.
How do you think of this paradox? Write an essay of no more than 1000 words.