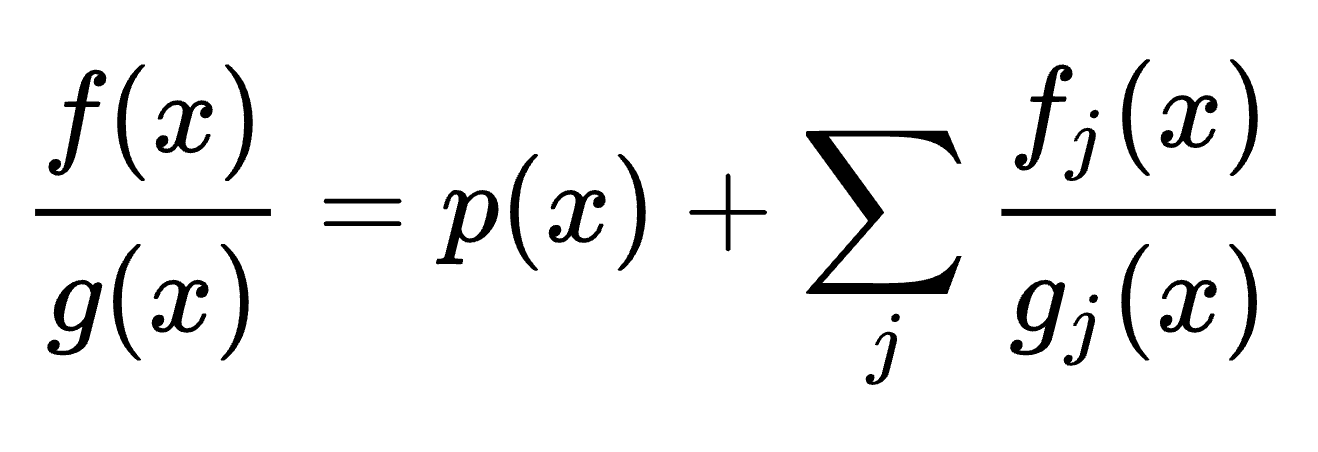A fast method for partial fraction decomposition¶
Generated by AI
该方法适用于口算
口算案例¶
对于
\[
\frac{3x^2-x}{(x+1)(x-1)^2}=\frac A{x+1}+\frac B{x-1}+\frac C{(x-1)^2}
\]
有
\[
A=\frac{3+1}{4}=1
\]
\[
C=\frac{3-1}{2}=1
\]
将 \(x=0\) 带入有
\[
0=1-B+2
\]
所以 \(B=2\),
\[
\frac{3x^2-x}{(x+1)(x-1)^2}=\frac 1{x+1}+\frac 2{x-1}+\frac 1{(x-1)^2}
\]
针对重根的“特值法”应用¶
假设有理分式包含一个 \(k\) 阶重根 \(r\),分解式包含以下部分:
\[
\frac{P(x)}{(x-r)^k Q_1(x)} = \frac{A_k}{(x-r)^k} + \frac{A_{k-1}}{(x-r)^{k-1}} + ... + \frac{A_1}{x-r} + \frac{\text{Other terms}}{Q_1(x)}
\]
1. 快速求出最高次项系数 \(A_k\)¶
为了求 \(A_k\),我们执行以下“特值”操作:
- 将等式两边同乘以 \((x-r)^k\)。
\[
\frac{P(x)}{Q_1(x)} = A_k + A_{k-1}(x-r) + ... + A_1(x-r)^{k-1} + \frac{\text{Other terms}}{Q_1(x)} \times (x-r)^k
\]
- 代入特值 \(x = r\)。
由于等式右边除了 \(A_k\) 之外的所有项都包含 \((x-r)\) 因式,所以它们都等于零。
\[
A_k = \left. \frac{P(x)}{Q_1(x)} \right|_{x=r}
\]
这就是留数法中求高阶极点最高次留数的思想。
2. 求解其他系数 (\(A_{k-1}\) 到 \(A_1\))¶
特值法在求出 \(A_k\) 后就失效了。要继续求解 \(A_{k-1}, A_{k-2}, ...\),通常需要结合其他方法:
| 方法 | 描述 | 特点 |
|---|---|---|
| 微分法/泰勒展开法 | 基于留数定理的思想,对 \(\dfrac{P(x)}{Q_1(x)}\) 进行逐级求导和代入 \(x=r\)。 | 最系统,效率高。能依次求出 \(A_{k-1}, A_{k-2}, ...\)。 |
| 代入其他任意值 | 求解 \(A_k\) 后,代入其他简单的特值,如 \(x=0, x=1, x=-1\) 等,得到关于 \(A_j\) 的线性方程组,然后结合待定系数法解出。 | 最容易理解和操作,但效率不如微分法。当系数不多时是好选择。 |
| 移项代入法 | 求出 \(A_k\) 后,将 \(\dfrac{A_k}{(x-r)^k}\) 移到左边,通分后,由于左边是真分式,新的分子应该包含 \((x-r)\) 因式,消去后得到一个更简单的分解式,再用同样的方法解下一项 \(A_{k-1}\)。 | 步骤繁琐,但避免了求导和解方程组。 |
例子演示(特值法 + 补充方法)¶
问题: 分解 \(R(x) = \dfrac{x}{(x-1)^2 (x+2)}\)。
步骤 1: 设定分解形式。 根有 \(r_1=1\)(2阶重根)和 \(r_2=-2\)(单根)。
\[
\frac{x}{(x-1)^2 (x+2)} = \frac{A_2}{(x-1)^2} + \frac{A_1}{x-1} + \frac{B}{x+2}
\]
步骤 2: 使用特值法求单根系数 \(B\)。
- 乘 \((x+2)\) 并代入 \(x=-2\):
\[
B = \left. \frac{x}{(x-1)^2} \right|_{x=-2} = \frac{-2}{(-2-1)^2} = \frac{-2}{9}
\]
步骤 3: 使用特值法求重根最高次系数 \(A_2\)。
- 乘 \((x-1)^2\) 并代入 \(x=1\):
\[
A_2 = \left. \frac{x}{x+2} \right|_{x=1} = \frac{1}{1+2} = \frac{1}{3}
\]
步骤 4: 求解 \(A_1\)(补充方法:代入其他任意值)。
- 现在我们有 \(A_2=\dfrac13\) 和 \(B=-\dfrac29\)。我们代入另一个简单的特值,例如 \(x=0\)。
\[
\left. \frac{x}{(x-1)^2 (x+2)} \right|_{x=0} = \frac{A_2}{(0-1)^2} + \frac{A_1}{0-1} + \frac{B}{0+2}
\]
\[
0 = \frac{1/3}{1} - A_1 + \frac{-2/9}{2}
\]
\[
0 = \frac{1}{3} - A_1 - \frac{1}{9}
\]
\[
A_1 = \frac{1}{3} - \frac{1}{9} = \frac{3}{9} - \frac{1}{9} = \frac{2}{9}
\]
最终分解式:
\[
\frac{x}{(x-1)^2 (x+2)} = \frac{1/3}{(x-1)^2} + \frac{2/9}{x-1} - \frac{2/9}{x+2}
\]
所以,特值法对于重根仍然是一个关键且快速的步骤,但它通常需要与其他方法(如微分或代入其他点)结合使用才能完成整个分解。